Ejemplos de Suma De Fracciones
Última modificación por: Redacción ejemplosde.com, año 2021
En Matemáticas, hay tres casos generales que se aplican en la suma de fracciones:
- Cuando todas las fracciones tienen el mismo denominador
- Cuando las fracciones tienen denominadores diferentes
- Cuando hay fracciones mixtas, es decir, con un número entero
A continuación, se describen ejemplos de cada uno de los casos:
Ejemplos de suma de fracciones con el mismo denominador
Estos ejercicios son los más sencillos. El denominador, que es el número debajo de la línea de la fracción, indica la naturaleza de las fracciones: nos dice si las fracciones son medios, tercios, cuartos, quintos, sextos, séptimos, octavos. Si en un ejercicio todos los denominadores son iguales, entonces se podrá hacer la suma directa de los numeradores.
Ejemplo 1:
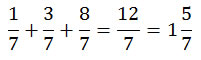
En este ejercicio, podemos notar que sólo se están sumando séptimos, por el denominador 7, que los caracteriza. Si estamos hablando de séptimos, entonces sabremos que el resultado también será en séptimos. Sólo hacemos la suma: 1 + 3 + 8, que son los numeradores de las fracciones. El resultado son 12 séptimos.
Sabemos que 1 entero contiene 7 séptimos (7/7). Si el resultado tiene un numerador mayor, se puede transformar en una fracción mixta: los enteros que se hayan completado, acompañados de los séptimos que hayan quedado. Se ha completado un entero, y le acompañan 5/7. Es otra forma correcta de expresar el resultado.
Ejemplo 2:
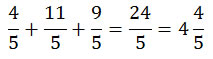
En este ejercicio, podemos notar que sólo se están sumando quintos, por el denominador 5, que los caracteriza. Si estamos hablando de quintos, entonces sabremos que el resultado también será en quintos. Sólo hacemos la suma: 4 + 11 + 9, que son los numeradores de las fracciones. El resultado son 24 quintos.
Sabemos que 1 entero contiene 5 quintos (5/5). Si el resultado tiene un numerador mayor, se puede transformar en una fracción mixta: los enteros que se hayan completado, acompañados de los quintos que hayan quedado. Se han completado cuatro enteros, y les acompañan 4/5. Es otra forma correcta de expresar el resultado.
Ejemplo 3:
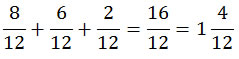
En este ejercicio, podemos notar que sólo se están sumando doceavos, por el denominador 12, que los caracteriza. Si estamos hablando de doceavos, entonces sabremos que el resultado también será en doceavos. Sólo hacemos la suma: 8 + 6 + 2, que son los numeradores de las fracciones. El resultado son 16 doceavos.
Sabemos que 1 entero contiene 12 doceavos (12/12). Si el resultado tiene un numerador mayor, se puede transformar en una fracción mixta: los enteros que se hayan completado, acompañados de los doceavos que hayan quedado. Se ha completado un entero, y le acompañan 4/12. Es otra forma correcta de expresar el resultado.
Ejemplos de suma de fracciones con denominadores diferentes
En estos ejercicios, los denominadores de las fracciones son diferentes. Se pueden estar sumando medios con sextos, con quintos. Aquí hay que evitar la suma directa de numeradores, porque sería como estar sumando peras con uvas y con naranjas.
Se necesitan tres pasos para resolver estas sumas de fracciones:
- Encontrar un denominador común para las fracciones
- Ajustar las fracciones al denominador común
- Ya que se tienen los mismos denominadores: sumar directo los numeradores
Ejemplo 1:
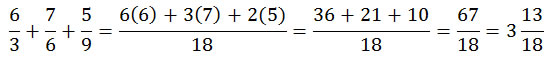
Paso 1: El denominador común se puede empezar a calcular multiplicando los dos primeros denominadores: 3x6=18. En este caso, resulta que el 18 es también múltiplo de 9, el de la última fracción. Nos quedamos con el 18 como denominador para nuestro ejercicio.
Paso 2: Para ajustar las fracciones al denominador común, hay que dividir el 18 entre cada denominador: 18 entre 3 = 6, 18 entre 6 = 3 y 18 entre 9 = 2. Estos resultados hay que multiplicarlos por sus respectivos numeradores, quedando: 6 por 6, 3 por 7 y 2 por 5. Así ya tendremos nuestras fracciones ajustadas a dieciochoavos.
Paso 3: Después de haber conseguido que todas las fracciones estuvieran ya en dieciochoavos, con sus numeradores ajustados, ya se suman todos ellos: 6(6)=36, 3(7)=21, 2(5)=10. Tenemos un resultado de 67/18.
Sabemos que 1 entero contiene 18 dieciochoavos (18/18). Si el resultado tiene un numerador mayor, se puede transformar en una fracción mixta: los enteros que se hayan completado, acompañados de los dieciochoavos que hayan quedado. Se han completado tres enteros, y le acompañan 13/18. Es otra forma correcta de expresar el resultado.
Ejemplo 2:
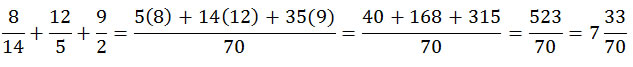
Paso 1: El denominador común se puede empezar a calcular multiplicando los dos primeros denominadores: 14x5=70. En este caso, resulta que el 70 es también múltiplo de 2, el de la última fracción. Nos quedamos con el 70 como denominador para nuestro ejercicio.
Paso 2: Para ajustar las fracciones al denominador común, hay que dividir el 70 entre cada denominador: 70 entre 14 = 5, 70 entre 5 = 14 y 70 entre 2 = 35. Estos resultados hay que multiplicarlos por sus respectivos numeradores, quedando: 5 por 8, 14 por 12 y 35 por 9. Así ya tendremos nuestras fracciones ajustadas a setentavos.
Paso 3: Después de haber conseguido que todas las fracciones estuvieran ya en setentavos, con sus numeradores ajustados, ya se suman todos ellos: 5(8)=40, 14(12)=168, 35(9)=315. Tenemos un resultado de 523/70.
Sabemos que 1 entero contiene 70 setentavos (70/70). Si el resultado tiene un numerador mayor, se puede transformar en una fracción mixta: los enteros que se hayan completado, acompañados de los setentavos que hayan quedado. Se han completado siete enteros, y le acompañan 33/70. Es otra forma correcta de expresar el resultado.
Ejemplos de sumas de fracciones con fracciones mixtas
Las fracciones mixtas son aquellas que expresan tanto con enteros como con fracciones propias. Estas son la alternativa a las fracciones impropias, cuyo numerador es mayor a su denominador. Por ejemplo:
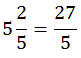
Ambas fracciones valen exactamente lo mismo; las dos hablan de quintos (denominador 5). La primera es una fracción mixta porque indica que hay 5 enteros, acompañado a 2/5. La segunda incluye todos los quintos que hay, en una sola fracción; es una fracción impropia. Las sumas que veremos a continuación comienzan con sus fracciones en la primera forma.
Estas sumas requieren de tres pasos principales para realizarse:
- Convertir las fracciones mixtas en impropias
- Si los denominadores son diferentes, conseguir uno común
- Sumar los numeradores y ponerles el denominador común
Ejemplo:
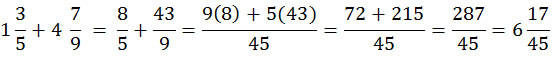
Paso 1: Las fracciones mixtas se transforman a impropias. El denominador se multiplica por el entero. Quedan: 5 por 1 = 5; 9 por 4 = 36. Estos resultados se suman a las fracciones propias que acompañaban al entero. Quedan: 5 + 3 = 8 quintos; 36 + 7 = 43 novenos. Estas fracciones son las que se van a sumar.
Paso 2: Si las fracciones impropias tienen denominador diferente, se consigue un denominador común. En este caso, para que se sumen quintos y novenos, hay que multiplicar los denominadores: 5 x 9 = 45. El 45 es el denominador con el que se hará la operación. Para ajustar los numeradores de las fracciones, el procedimiento es:
- Se divide el 45 entre cada numerador: 45 entre 5 = 9; 45 entre 9 = 5.
- El 9 y el 5 van a multiplicar a los numeradores 8 y 43: 9(8)=72, 5(43)=215.
Paso 3: Ya con el denominador 45, se suman 72 + 215, que son los numeradores. Tenemos como resultado 287/45.
Sabemos que 1 entero contiene 45/45. Si el resultado tiene un numerador mayor, se puede transformar en una fracción mixta: los enteros que se hayan completado, acompañados de los “45avos” que hayan quedado. Se han completado seis enteros, y le acompañan 17/45. Es la forma correcta de expresar el resultado como fracción mixta.
