Ejemplos de Triángulo De Pascal

El triángulo de Pascal, también llamado Triángulo de Tartalio, es una formación de números que a través de su acomodo entrega revelaciones como:

• En álgebra, los coeficientes de un binomio a la “n” potencia. El exponente “n” será el renglón del triángulo que habrá que observar.
• Sucesión de Fibonacci: dos números consecutivos tienen debajo su suma, en el siguiente renglón.

¿Cómo se forma el triángulo de Pascal?

Para crear el Triángulo de Pascal, hay que guiarse con los siguientes pasos:

• Se conforma desde la punta con un 1.
• El siguiente renglón son 1, 1.
• Sigue la suma de ellos, a cuyos extremos van 1, 1 (1 – 2 – 1).
• Sigue la suma de ellos, y a los extremos 1, 1 (1 – 3 – 3 – 1).
• Sigue la suma de ellos, y a los extremos 1, 1 (1 – 4 – 6 – 4 – 1).
• Así sucesivamente hasta el infinito.

Ejemplos de Triángulo de Pascal

Se describe cada una de las utilidades que tiene el Triángulo de Pascal.

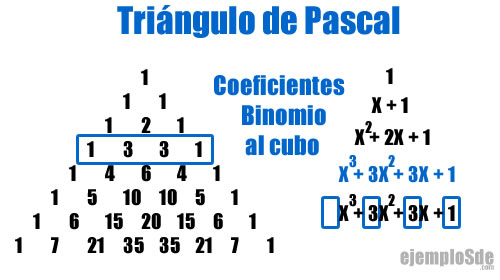
Binomio a la “n” potencia

Cuando un binomio es elevado a una potencia ”n”, cada término del resultado tendrá un coeficiente determinado. Esto acortará el proceso de resolverlo, y no se tendrá que multiplicar término a término para llegar al resultado.

Hay que tomar en cuenta lo siguiente:

• En el binomio al cuadrado (x + a)² = (x + a)*(x + a), por ejemplo, la regla es: “Cuadrado del primer término, más el doble producto del primero por el segundo, más el cuadrado del segundo”: x² + 2ax + a².
• La punta del triángulo es el renglón 0: la potencia 0. Todo binomio (todo número, tal cual) elevado a la potencia 0 equivale a 1. El siguiente renglón es para la potencia 1. Ambos términos del binomio tienen coeficientes 1. El siguiente renglón es para la potencia 2. Los coeficientes alternan 1, 2, 1, como se observa en el ejemplo: x² + 2ax + a² = 1x² + 2ax + 1a². Y así sucesivamente con las demás potencias.

Sucesión de Fibonacci

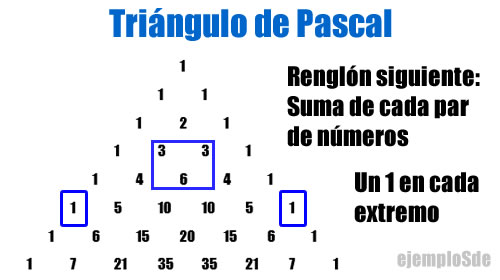
Cada renglón del Triángulo de Pascal está conformado por las sumas de cada dos de los números superiores. Hay un 1 en el extremo izquierdo y otro 1 en el extremo derecho. De ahí parte el concepto de la llamada Sucesión de Fibonacci, en la cual se parte desde el 0, sigue el 1 y cada número siguiente es el resultado de la suma de los dos anteriores. La sucesión dice: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Sigue con:

• Binomios
• Binomio al cuadrado
• Trinomio cuadrado perfecto
• Coeficiente