Ejemplos de Números Imaginarios

Inicio » Matemáticas » Números imaginarios
Última modificación por: Redacción ejemplosde.com, año 2021

Los números imaginarios o números complejos son los que llevan la raíz cuadrada de un número negativo. Establecen la llamada unidad imaginaria, que es el número √-1 (raíz de -1) y se designa por la letra i.

Unidad imaginaria: √-1 = i

Características de los números imaginarios

Llevan una parte real, que puede ser cualquier número real. Esta parte se señala con la letra b. Acompaña a la unidad imaginaria como un coeficiente, y se escribe b i.
Por ejemplo: 5i, 2i, 3i.
Con los números imaginarios se pueden calcular raíces con índice par (raíz cuadrada, cuarta, sexta, etc.) y radicando negativo (el número de dentro).
Por ejemplo: √-9 = √(9*-1) = 3 * √-1 = 3i.
También se pueden presentar en forma de binomio, en la manera a + bi. La letra a será la parte real y la b acompañará la parte imaginaria.
Si i se eleva al cuadrado, se retirará la raíz y quedará: i² = -1 e irá tomando diferentes valores según la potencia a la que se eleve.

Potencias de la unidad imaginaria

Cuando i se eleva a una potencia, arrojará un valor determinado:

i⁰ = 1

i¹ = i

i² = -1

i³ = -i

i⁴ = 1

Se detallan con las siguientes explicaciones:

i⁰ = 1 : Todo número elevado a la potencia 0 es igual a 1. Es también el caso de i.
i¹ = i : Un número elevado a la potencia 1 es igual a sí mismo.
i² = -1 : La unidad imaginaria i vale √-1, de manera que al elevarla al cuadrado se quitará la raíz y se obtendrá el -1 de adentro.
i³ = -i : Se pueden desglosar los exponentes como i³ = i² * i, y en esta expresión sustituir sus valores i³ = (-1) * i. Se comprueba que i³ = -i.
i⁴ = 1 : Se pueden desglosar los exponentes como i⁴ = i² * i² y en esta expresión sustituir sus valores i⁴ = -1 * -1. Se comprueba que i⁴ = 1.

Los valores se van repitiendo de cuatro en cuatro, por lo que, para saber cuánto vale una potencia de i cualquiera, se divide el exponente entre 4, y el residuo de la división será el exponente que nos dirá cuál es el valor.

Por ejemplo:

i³⁸ = i³⁶ * i²= (i⁴)⁹ * i² = -1

i⁴³ = i⁴⁰ * i³ = (i⁴)¹⁰ * i³ = -i

i²² = i²⁰ * i² = (i⁴)⁵ * i² = -1

i¹⁸ = i¹⁶ * i² = (i⁴)⁴ * i² = -1

i¹⁹ = i¹⁶ * i³ = (i⁴)⁴ * i³ = -i

Forma binómica de los números imaginarios

Los números imaginarios en su forma binómica también son llamados números complejos. Tienen todos ellos la estructura siguiente:

a + bi

Este conjunto numérico se representa con la letra C y se expresa: C = {a + bi / a,b Є R}

Se lee de la siguiente forma:

“Los números complejos son todos aquellos en la forma a + bi, donde a y b están en el conjunto de los números reales R”

Los números complejos tienen una serie de reglas que vuelven más fácil su comprensión:

Si a = 0, el número queda como bi, y se dice que es un número imaginario puro.
Si b = 0, el número queda como a, un número real. Se comprueba como a + 0i = a.
Los números complejos a + bi y –a – bi se llaman opuestos.
Los números complejos a + bi y a – bi se llaman conjugados.
Dos números complejos son iguales cuando tienen la misma componente real y la misma componente imaginaria.

Operaciones de los números imaginarios

Los números imaginarios participan en las operaciones matemáticas básicas:

Suma
Resta
Multiplicación
División

En la suma de números imaginarios o complejos, se ordenan las partes reales por un lado y las partes imaginarias aparte. Se acumulan y el resultado será otro número imaginario, con su parte real y su parte imaginaria. Esta operación se representa de la siguiente manera:

(a + bi) + (c + di) = (a + c) + (b + d)i

Por ejemplo:

(5 + 2i) + (–8 + 3i) = (5 – 8) + (2 + 3)i = –3 + 5i
(–2 + 4i) + (7 – 6i) = (–2 + 7) + (4 – 6)i = 5 – 2i
(10 – 3i) + (–4 + 9i) = (10 – 4) + (–3 + 9)i = 6 + 6i
(21 – 4i) + (10 + 5i) = (21 + 10) + (–4 + 5)i = 31 + i
(3 + i) + (–1 + 5i) = (3 – 1) + (1 + 5)i = 2 + 6i

En la resta de números imaginarios o complejos, se agrupan las partes reales en un término, y las partes imaginarias en otro. Los signos afectados por la resta se modifican. Así, se van a acumular ya directamente, respetando las Leyes de los signos. Se representa de la siguiente manera:

(a + bi) – (c + di) = (a + c) – (b + d)i

Por ejemplo:

(5 + 2i) – (–8 + 3i) = [5 – (–8)] + (2 – 3)i = 13 – i
(–2 + 4i) – (7 – 6i) = (–2 – 7) + [4 – (–6)]i = –9 + 10i
(10 – 3i) – (–4 + 9i) = [10 – (–4)] + (–3 – 9)i = 14 – 12i
(21 – 4i) – (10 + 5i) = (21 – 10) + (–4 – 5)i = 11 – 9i
(3 + i) – (–1 + 5i) = [3 – (–1)] + (1 – 5)i = 4 – 4i

En la multiplicación de números imaginarios o complejos, se aplica la propiedad distributiva, multiplicando cada parte real por cada parte imaginaria. Se respetan las Leyes de los signos y se tiene en cuenta que i² = –1. Se representa de la siguiente manera:

(a + bi) * (c + di) = (ac – bd) + (b + d)i

Por ejemplo:

(5 + 2i) * (–8 + 3i) = (5)(-8) + (5)(3i) + (2i)(-8) + (2i)(3i) = –40 + 15i –16i + 6i² = –40 + (15 – 16)i + 6(–1) = (–40 –6) + (–1)i = –46 –i
(–2 + 4i) * (7 – 6i) = (–2)(7) + (–2)( –6i) + (4i)(7) + (4i)( –6i) = –14 + 12i + 28i – 24i² = –14 + (12 + 28)i – 24(–1) = (–14 + 24) + (40)i = 10 + 40i
(10 – 3i) * (–4 + 9i) = (10)( –4) + (10)(9i) + (–3i)( –4) + (–3i)(9i) = –40 + 90i + 12i – 27i² = –40 + (90 + 12)i – 27(–1) = (–40 + 27) + (102)i = –13 + 102i
(21 – 4i) * (10 + 5i) = (21)(10) + (21)(5i) + (–4i)(10) + (–4i)(5i) = 210 + 105i –40i – 20i² = 210 + (105 – 40)i – 20(–1) = (210 + 20) + (65)i = 230 + 65i
(3 + i) * (–1 + 5i) = (3)(–1) + (3)(5i) + (i)( –1) + (i)(5i) = –3 + 15i –i + 5i² = –3 + (15 – 1)i + 5(–1) = (–3 – 5) + (15–1)i = –8 + 14i

En la división de números imaginarios o complejos, se racionaliza el denominador. Es decir, el divisor y el dividendo se multiplican por el conjugado del denominador, de esta manera:

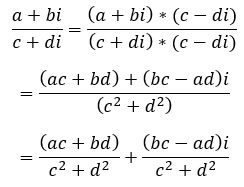
División de números imaginarios

Por ejemplo:

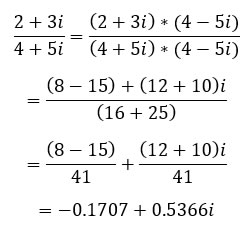
Ejemplo de división de números imaginarios